知科学の中でもっとも重要なものの1つがこの計算論(あるいは記号論)です。
この発想のベースにはホッブスの「心の営みとは、心的な記号系(心的表象系)を処理、操作することである」という主張があって、その点から多彩な心理現象を見ようとしています。
ここでいう計算とは算数の四則演算(足し算、引き算、掛け算、割り算)に似たようなものです。
たとえば、国語は基本的な記号「文字」を「適切に結合」して「語」を作ります。そして「文」はその「語」と「語」を「適切に結合」したもの。その「文」をさらに「文」と「適切に結合」させると、このように文章になります。この考え方が計算論です。
もちろんこの計算にはルールが存在します。国語とか英語とか、そういうものなら文法や話者、著者の直感が1つのルール(法則)です。
人間にとっての身近な記号といえば、たとえば文字とか数字とか図形とか、標識なんかのマークとか、絵文字とか、それはもういろいろあります。このうち文字や数字は「内言」という形で現れてくることもあります(たとえば、読んでいる文字を頭の中で言う)。
また人間の頭の中にあるイメージや象徴も記号といえます。これらは「内的表象系」といいます。
これらを取捨選択、判断、意思決定、評価、修正、記憶など操作すること、それが心の役割と考えます。
つまり、計算論をまとめるとこういうことになります。
- 心は記号の処理・操作系である。
- 処理・操作とは計算であり、任意の記号と記号を一定の規則にしたがって結合する操作を指す。この規則の基となるものを論理構造という。
- 記号の集まりである記号系と、個々の記号と記号を結びつける規則の集まり(規則系(集合))、これらの総体は現実の意味論である。
- このような特性を持つ「機械」は具体的に作ることができる。
最初の2つは先ほどまでで説明しましたが、3番目に「意味論」という新しい言葉が出てきています。
ここでいう意味論とは「パースの意味論」です。いくつかの側面があるのでそれぞれ説明しましょう。
まず1つ目が「記号と記号の指示対象関係に関わる」狭義の意味論です。たとえば、「机」という語は「面があって、足があって…」という指示対象が意味するように意味します。この考え方が狭義の意味論です。
2つ目は「語の意味に関するもの」語用論と言ったりします。たとえば、人の背中を机代わりにして何か書くなんてとき、背中は机になっているわけですが、このような観点からのものの見方が語用論です。
3つ目は構文論。記号と記号の間の関係構造を指すものでして、記号論における心の意味はこれに当たります(記号系+規則系=意味)。
ややこしいですが、図にするとこういうこと。
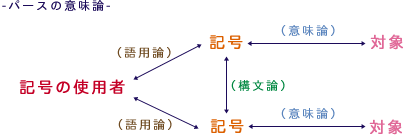
ということで、ここでは構文論にスポットを当てましょう。そのために、超単純な「三段論法」を考えてみます。
ちなみに三段論法とは、「人はいつか死ぬ そして私は人である ゆえに私はいつか死ぬ」(ダークだな(^^;))みたいなもののことで、ここの「~は~である」という主語と述語でできた文を「命題」、その一番最初のものを「大前提」、次を「小前提」、最後を「結論」といいます。導き方としてはA→B→C。このB→Cの過程が「推理」です。
この命題「~は~である」というのは交換可能です。つまり、「~でない」という否定もありえます。よって、
すべてのsはpである(sap) / すべてのsはpではない(sep) / あるsはpである(sip) / あるsはpではない(sop)
これらがあり得、その可能な組み合わせは、
格(図式)
|
1
|
2
|
3
|
4
|
大前提
|
MP
|
PM
|
MP
|
PM
|
小前提
|
SM
|
SM
|
MS
|
MS
|
結論
|
sp
|
sp
|
sp
|
sp
|
(これらそれぞれの間にa,e,i,oのどれからが入る)
から、大前提、小前提、結論それぞれで4タイプ、つまり256通りありえます。このうち論理的に可能なのをa,e,i,oだけで表すと(これをアリストテレスが発見したのでアリストテレス論理学という)、
1) aaa, eae, aii, eio 2) eae, aee, eio, aoo 3) aai, iai, aii, eao, oao, eio 4) aai, aee, iai, eao, eio
の19通り(重複を除くと10通り)。そのうち誤りが2つ(第3格のaaiとeao。アリストテレスの発見から2千数百年後にブールが発見(ブール代数)、現代記号論理学につながる)あることがわかっています。
もう大半の人がついてこれなくなっていると思いますが、今、人間の思考過程を数学にしようとしているのです。そして、この現代記号論理学が、計算論には重大なパワーを持ちます。
先ほど計算は四則演算に似ているといいましたが、これを具体的にしてみましょう。
ここで、任意の命題p、qに対して、条件文「~して、~だ」をAND、「~、あるいは~」をOR、「~ではない」をNOT、「~なら~だ」をIF-THENで表します。この命題p、qは「真か偽か yes or no」のどちらかなので、2進数に置き換えると、実はこの条件文、2進数の計算になります。
p
|
q
|
p and q
(x) |
p or q
(+) |
not p
(1-p) |
not q
(1-q) |
if p, then q
p(1-q)=0 |
1
|
1
|
1
|
10
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
何をやったかわかりますか? これは心の働きを計算に置き換えたのです。
この2値の処理にスイッチを用いれば電気的な回路になり(回路図は略)、発展させればプログラムになります。サンプルにCで「1000円未満のおつりに最適な硬貨の枚数を10円単位で求めるプログラム」を書いてみましょう(ソースの中に書いてあるので解説はしません。コンパイルすれば一応、動くはず)。
#include <stdio.h>
main(){
int money;
int yen500 = 0,yen100 = 0,yen50 = 0,yen10 = 0;
printf("お釣りの金額を入力してください(1000円未満10円単位で) : ");
scanf("%d",&money);
/*500円以上の時、500円玉の枚数を求める*/
if(money >= 500){
yen500 = 1;
/*ここで、次のif文に引き渡す額を計算、moneyに代入*/
money = money - 500;
}
/*100円以上の時、100円玉の枚数を求める*/
if(money >= 100){
yen100 = money / 100;
/* %は、あまりを求めるときの演算子 */
money = money % 100;
}
/*50円以上の時、50円玉の枚数を求める*/
if(money >= 50){
yen100 = 1;
money = money - 50;
}
/*10円以上の時、10円玉の枚数を求める*/
yen10 = money / 10;
printf("500円が%d枚、100円が%d枚、50円が%d枚、10円が%d枚です。\n",yen500,yen100,yen50,yen10);
}
このアプローチは命題論理学がベースなのですが、これより深くへは「述語論理学」などを知らないとダメです。「ゲーテルの不完全性定理」とか、「オートマトン(自動機械)」とか、「チューリングマシン」とか、ありとあらゆるものを説明するところからはじめないといけないのでここでは割愛。
ただ、「心=計算」と認知科学は考えていて、それが「人工知能 artificial intelligence」なんてのにつながっていることは覚えておいてください。
ちなみにオートマトンとか、チューリングマシン、その前にチューリングって言う人については、技術評論社「あなたはコンピュータを理解していますか?(梅津信幸・著)」あたりがわかりやすいと思いますので、ご参考までに。
0 件のコメント:
コメントを投稿